ОБЩАЯ ХАРАКТЕРИСТИКА АТМОСФЕРНОЙ ТУРБУЛЕНТНОСТИ

В § 1.1 указывалось, что для оценки воздействия на полет самолета скорость ветра условно рассматривается в виде суммы двух составляющих — постоянной и переменной. Переменная со­ставляющая скорости ветра и характеризует турбулентность атмосферы. Турбулентным принято называть неупорядоченное, хаотическое движение воздуха в атмосфере. В данной книге будет рассматриваться такое турбулентное движение воздуха, при котором скорости в любой рассматриваемой точке области, где это движение имеет место, являются случайными функциями координат этой точки и времени, причем функциями, которые могут быть описаны методами теории вероятности [7].

Непосредственной причиной возникновения турбулентности’ в атмосфере являются вертикальные и горизонтальные градиенты температуры и скорости ветра. В работе [8] указываются следую­щие явления, обуславливающие турбулентный характер движе­ния воздуха в атмосфере:

1) трение воздушного потока о поверхность земли и местные предметы, вызывающие появление вертикальных и горизонталь­ных градиентов скорости ветра;

2) вертикальные потоки воздуха, обусловленные неодинако­вым нагревом различных участков земной поверхности; эти пото­ки порождают так называемую термическую или конвекционную турбулентность;

3) процессы облакообразования, связанные с появлением зна­чительных градиентов температуры и скорости ветра;

4) взаимодействие воздушных масс с различным термическим режимом, формирующих атмосферные фронты с большими гори­зонтальными градиентами температуры и скорости ветра;

5) большие градиенты ветра на границах струйных течений;

6) деформация воздушных течений горами и возвышенно­стями.

По происхождению, характеру и энергетическим процессам весь диапазон движений воздуха в атмосфере может быть разбит на три интервала:

1) интервал крупномасштабных движений воздуха;

2) инерционный интервал;

3) вязкий интервал.

Основная часть солнечной энергии, за счет которой поддер­живается турбулентное движение, вносится в атмосферу движе­ниями крупномасштабного интервала. Эти движения обуслов­лены нарушением равновесного состояния атмосферы при нерав­номерном нагреве ее за счет прямой и отраженной солнечной радиации. Хотя эти горизонтальные крупномасштабные движе­ния воздуха, как указывалось выше, также имеют турбулентный характер, однако при изучении динамики полета они могут рас­сматриваться как ветры постоянной скорости.

Очевидно, что в этом крупномасштабном интервале движение воздуха имеет четко выраженную анизотропию, обусловленную ограничивающим влиянием земной поверхности и зависимостью характеристик атмосферы от высоты данной точки над этой по­верхностью.

Энергия крупномасштабных движений передается порывам ветра более мелкого масштаба, которые обычно относят к инер­ционному интервалу турбулентности. В этом интервале вихревое движение воздуха теряет непосредственную связь с вызвавшим его крупномасштабным движением воздуха.

Вихревые порывы в инерционном диапазоне не имеют пред­почтительного направления и в статистическом смысле их можно рассматривать как изотропные. Естественно, что размеры наи­больших вихрей, относящихся к инерционному интервалу, зави­сят как от высоты рассматриваемой точки атмосферы, так и от метеорологических условий, вызвавших турбулентность. Непо­средственно к земной поверхности примыкает пограничный слой, высота которого в зависимости от метеорологических условий колеблется в пределах нескольких сотен метров [9]. Выше распо­лагается так называемая свободная атмосфера, для которой пре­дельно большие размеры вихрей в инерционном интервале изме­ряются величинами от нескольких сотен метров [10] до нескольких километров [48].

Предельно малые размеры вихрей в инерционном интервале ограничены вязким интервалом, охватывающим область наиболее высоких частот движения частиц воздуха. В вязком интервале происходит превращение основной части механической энергии в тепловую за счет сил вязкого трения. В работе [9] приведены дан­
ные относительно граничных размеров вихрей вязкого интервала. Для свободной атмосферы размеры этих вихрей измеряются не­сколькими сантиметрами. Таким образом, инерционный интервал турбулентного движения в атмосфере охватывает диапазон вих­рей от нескольких сот метров (или нескольких километров) до нескольких сантиметров и представляет наибольший интерес в смысле воздействия на динамику современных самолетов. По мере роста скоростей полета самолетов все большее значение для динамики полета приобретают порывы большей протяженности, лежащие за пределами инерционного диапазона.

Если в процессе преобразования механической энергии круп­номасштабных движений атмосферы в энергию теплового движе-

W0 і Профиль среднего

9 о о

р I SJ Турбулентность

а О

а mm*

ния молекул газов, входящих в состав воздуха, поступает больше энергии, чем выделяется, то избыток энергии идет на увеличение интенсивности турбулентного движения. Если же в тепло пере­ходит больше энергии, чем ее поступает от крупномасштабных движений воздуха, то турбулентность вырождается. Однако процессы развития и вырождения турбулентности являются до­статочно длительными и с точки зрения воздействия на быстро летящий самолет турбулентность обычно рассматривается как установившийся, т. е. сбалансированный в энергетическом отно­шении процесс. Поэтому в данной книге не будут рассматривать­ся вопросы динамики турбулентности.

Приведем некоторые данные о конкретных видах турбулент­ности атмосферы.

Турбулентность в пограничном с земной поверхностью слое атмосферы возникает в результате взаимодействия потока с зем­ной поверхностью, действия конвективных потоков воздуха и влияния вертикальных и горизонтальных градиентов скорости ветра и температуры. На рис. 1.5 показана схема турбулентного
потока в приземном слое. На высотах, близких к высоте пре­пятствий и ниже, турбулентность в некоторой степени отражает геометрическую форму этих препятствий. По мере увеличения высоты турбулентное движение воздуха становится случайным.

Характеристики потока в приземном слое [9] при безразлич­ной стратификации атмосферы[2] не должны существенно отли­чаться от достаточно хорошо исследованных характеристик в турбулентном пограничном слое на плоской пластинке, продувае­мой в аэродинамической трубе. Однако при изменении стратифи­кации на устойчивую или неустойчивую характеристики движе­ния воздух» в пограничном слое изменяются весьма существенно.

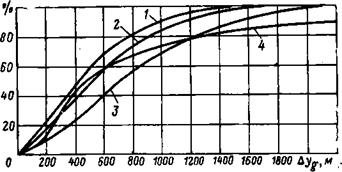
Рис. 1.6. Повторяемость толщин турбулентных зон: 1 — данные для северных широт СССР; 2 — данные для умеренных ши­рот СССР; 3 —данные для южных широт СССР; 4 —канадские данные

Хотя изучение этих характеристик и ведется достаточно интен­сивно, оно еще далеко до своего завершения. Достаточно полный обзор имеющихся данных о турбулентности в приземном слое приведен в работе [9].

В начале этого параграфа были указаны причины возникнове­ния турбулентности в свободной атмосфере. Турбулентные зоны в свободной атмосфере располагаются в виде сравнительно тон­ких слоев, занимающих большие площади с довольно четкими границами.

На рис. 1.6 приведены кривые, характеризующие повторяе­мость в процентах толщин таких зон для Канады (кривая 4) и для различных широт Советского Союза (кривые 1—3) [8]. Графики показывают повторяемость толщин, меньших, чем значе­ния, отложенные по оси абсцисс. Кривые на рис. 1.6 показывают, что, например, толщины зон, меньшие 1000 м, встречаются в се­верных широтах Советского Союза приблизительно в 90% слу­чаев, в умеренных — в 85%, в Канаде — в 75% и в южных широтах — в 70% случаев. Максимальная толщина турбулентных зон почти никогда не превосходит 2000 м. Отсюда вытекает, что для выхода из зоны «болтанки» в тех случаях, когда это допу­стимо — по условиям полета, следует изменить высоту.

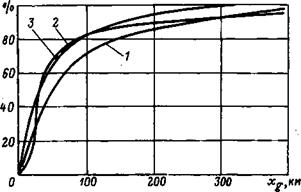
На рис. 1.7 приведены кривые {8] повторяемости горизонталь­ных размеров турбулентных зон. Смысл этих кривых тот же, что и кривых на рис. 1.6. Кривые на рис. 1.7 показывают, например, что для СССР протяженность турбулентной зоны, меньшая 20 км, встречается примерно в 20% случаев, а протяженность, меньшая 100 км, — в 70% случаев.

Рис. 1.7. Повторяемость горизонтальных размеров турбулентных зон: / — данные для умеренных широт СССР; 2 — канадские дан­ные; 5 —данные США

Следовательно, время полета самолета в турбулентных зонах довольно значительно и для современных самолетов измеряется минутами.

Зоны турбулентности обычно содержат облака или же распо­лагаются вблизи мощных кучевых облаков. Эти признаки преду­преждают экипажи самолетов о возможном попадании в турбу­лентную зону. Однако турбулентные зоны могут встретиться и при безоблачной погоде. Они возникают на границе струйного течения, а также при появлении местных градиентов скорости ветра, вызванных обтеканием воздухом горных хребтов. В насто­ящее время не существует бортовых средств для прогнозирования встречи с турбулентностью при ясной погоде, благодаря чему встреча с такой зоной является для экипажа самолета, как пра­вило, внезапной.

Наибольшую опасность для полета самолета представляет турбулентность при грозах. Летные инструкции для всех типов самолетов запрещают заход самолета в грозовые зоны. Положе­ние этих зон определяется наземными средствами метеослужбы, а также установленными на самолетах многих типов бортовыми

локаторами для обнаружения гроз. Несмотря на все это, бывают случаи попадания самолетов в грозовые зоны. Поэтому грозовая турбулентность исследуется достаточно интенсивно.

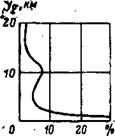
На рис. 1.8 приведено относительное расстояние полета в усло­виях турбулентности в зависимости от высоты (1]. Турбулентность условно разделена на грозовую и негрозовую. Следует иметь в виду, что графики на рис. 1.8 получены путем обработки боль­шого статистического материала и поэтому справедливы только для оценки средних условий при большом числе полетов. Эти графики объективно отражают вероятность встречи с турбулент­ностью по высотам с учетом мер по обходу или выходу из турбулентных зон. Эта поправка особенно сущест­венна для оценки условий попадания в грозовую тур­булентность. По мнению автора работы [1], действи­тельная протяженность гро­зовых зон на порядок вы­ше, чем показано на рис. 1.8, б, где кривые построены с учетом применяемых в по­летах мер по обходу гроз.

Как показывает график на рис. 1.8, а, наиболее ча­сто встречается турбулент­ность на малых высотах, т. е. термическая или конвенционная турбулентность. При увеличении высоты ‘вероятность полета в турбулентных условиях уменьшается. Лишь несколько ниже тропопаузы наблюдается некоторое увеличение этой вероятности из-за наличия на этой высоте струйных течений. Выше тропо­паузы и в нижней стратосфере вероятность попадания в зону турбулентности продолжает уменьшаться.

В заключение этого параграфа приведем табл. 1.1, в которой показано, как оценивается воздействие турбулентной атмосферы на самолет. Результат этого воздействия («болтанка») опреде­ляется по амплитуде нормальной перегрузки, испытываемой в полете.

Таблица 1J Характеристика. болганки" самолета Интенсивность. болтанки" в баллах Диапазон приращений перегрузки Слабая о* Дпу | <0,20 Умеренная о* Ал» | <0,50 Сильная аЗ ДЛу | <1,0 Штормовая о4 ДЛу | > 1,0

Представляют также интерес данные по оценке летчиками интенсивности турбулентности и соответствующие этой оценке среднеквадратичные значения вертикальной перегрузки. Эти дан­ные получены экспериментально в результате полетов на скоро­стных истребителях [49]. Они являются довольно грубыми и могут использоваться лишь для ориентировочной оценки интенсивности турбулентности.

Результаты исследований сведены в табл. 1.2.

Оценка летчиком интенсивности турбулентности	Среднеквадратичные значения перегрузки
Пренебрежимо слабая	0,05
Слабая	0,1
Умеренная	0,1—0,15
Сильная	0,2—0,3
Очень сильная	0,3

Таблица 1.2

§ 1.4. АНАЛИТИЧЕСКОЕ ОПИСАНИЕ КИНЕМАТИКИ ТУРБУЛЕНТНОГО ДВИЖЕНИЯ ВОЗДУХА В АТМОСФЕРЕ

Для исследования динамики полета в турбулентной атмосфере необходимо располагать аналитическим методом описания поля скоростей ветра. В настоящее время для описания неспокойной [3]

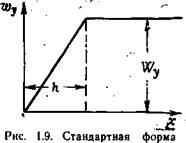
дискретного порыва

При указанных допущениях замеренные в полете прираще­ния вертикального ускорения Апу пересчитываются в скорости вертикальных порывов ветра по формуле

Wy= 2GIS — Дду, (1.4)

k? vc*

где G — вес самолета;

р — массовая плотность воздуха;

V — скорость полета;

5 — площадь крыла;

С* — производная по углу атаки от коэффициента подъемной силы;

k — коэффициент ослабления перегрузки за счет «градиент­ного участка» порыва.

Этот коэффициент вычисляется по формуле

1-е-‘1

V

<ygfh

v=————

2G/S

и g — ускорение силы тяжести.

При расчете Wy по формуле (1.4) в качестве Апу используют­ся амплитудные значения приращения перегрузки, зарегистри­рованные акселерометрами, устанавливаемыми на самолете при его нормальной эксплуатации или при полетах для исследова­ния турбулентной атмосферы.

Необходимо отметить, что вычисленная по формуле (1.4) скорость порыва не является истинной скоростью воздуха, так как допущения, сделанные при получении этой формулы, явля­ются достаточно грубыми. Однако предполагается, что использо­вание этих скоростей порывов при вычислении нагрузок от ветра для другого самолета дает приблизительно верные результаты. Из самого характера приведенных выше допущений следует, что метод дискретных порывов почти не связан с реальным характе­ром порывов ветра в атмосфере, и его применение может дать удовлетворительные результаты только для динамически подоб­ных самолетов.

В данной книге будет применяться второй метод, при котором используется статистическое описание поля скоростей ветра. Этот метод в настоящее время широко применяется в работах по динамике полета в неспокойной атмосфере. Статистический метод позволяет значительно точнее описать реальные процессы движе­ния воздуха в атмосфере, чем метод дискретного порыва, хотя также требует введения некоторых допущений. Эти допущения сводятся к следующему:

1) поле скоростей ветра на определенных участках турбулент­ной атмосферы является однородным и изотропным;

2) для летящего самолета поле скоростей ветра является «замороженным», т. е. не меняется со временем (гипотеза Тей­лора).

Более подробно смысл и значение указанных допущений будет раскрыт ниже.

Перейдем к аналитическому описанию поля скоростей ветра. Поскольку заранее оговорено, что рассматриваемая случайная составляющая скорости ветра является случайной функцией, то для ее полного описания необходимо получить корреляционную функцию или спектральную плотность, а также закон распреде­ления мгновенных значений скорости ветра.

Как уже неоднократно указывалось выше, полный вектор ветра W может быть условно представлен как сумма постоянной W0 и переменной w составляющих:

W=W0+w. (1.5)

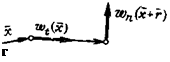
Ниже в этой главе_будет рассматриваться только переменная составляющая ветра w, которая считается случайной функцией времени и координат определенной точки поля. Рассмотрим две точкігполя скоростей в данный момент времени. При таком усло­вии w будет случайной функцией только координат пространства. Пусть одна точка поля определяется радиусом-вектором х, _а любая другая — вектором г, проведенным из конца вектора х. Будем полагать, что рассматриваемая турбулентность воздуха является однородной и изотропной. Под «однородной турбулент­ностью» понимается турбулентное движение, вероятностные ха­рактеристики которого одинаковы для всего рассматриваемого поля скоростей ветра. Под «изотропной турбулентностью» пони­мается турбулентное движение, вероятностные характеристики которого не зависят от направления г, по которому рассматри­вается корреляционная связь между скоростями в двух точках поля. Из общей теории однородной и изотропной турбулентности следует, что для описания поля скоростей в этом случае доста­точно знать две корреляционные функции для проекций вектора скорости на оси прямоугольных координат [11]. При эксперимен­тальном исследовании турбулентности в качестве таких функций берут корреляционные функции для проекций вектора скорости w на направления: совпадающее с вектором г (продольная), и перпендикулярное к нему (поперечная). Геометрический смысл этих проекций поясняется рис. 1.10, а. На основании рис. 1.10, а получаем выражения для продольной и поперечной корреляцион­ных функций [4]:

Rt(r)=w((x)wt(x4- г), (1.6)

Rn(r) = w„(x)wn (x + 7). (1.7)

Черта над произведением мгновенных значений скоростей в (1.6) и (1.7) обозначает операцию осреднения. Знак вектора в аргументе корреляционных функций опущен, так как в изотроп­ной турбулентности эти функции инвариантны к повороту векто­ра г. Функции Rt{r) и /?„(/•) не являются независимыми. Соглас­но [11] для изотропной и однородной турбулентности связь меж­ду этими функциями определяется соотношением

K„(r)~R,{.r) + ±r-?bp-. (1.8)

х т Щ(х+р)

На основании общей теории турбулентности [11] все перекрест­ные корреляционные функции вида (рис. 1.10,6) тождественно равны нулю:

^/n(r) = wt(x)wn(x-{-r)= 0, ]

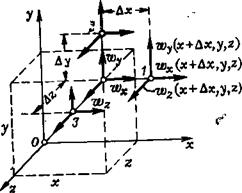
Найдем вид корреляционных функций для проекций вектора ветра ад на оси декартовых координат. Пусть вектор скорости ветра ад в точке с координатами х, у, z (рис. 1.11) имеет состав­ляющие адж(х, у, z), ад„(х, у, z), wz(x, у, z). Тогда в точке / с ко­ординатами х+Лх, у, z вектор скорости ветра будет иметь проек­ции ад*(х+Дх, у, z), ад„(х+Дх, у, z), адг(х+Ах, у, г). Соответ­ственно, в точке 2 с координатами х, у+Ау, z проекции будут иметь вид ад*(х, у+Ау, z), wy(x, у + Ау, z), wz(x, у+Ау, г), и в
точке 3 с координатами х, у, z+Az — wx(x, у, z+Az), wy(x, у, z+ +Аz), u>z(x, у, z+Az) *.

Сравнивая расположение проекций векторов скорости на рис. 1.11 и 1.10, на основании формул (1.6), (1.7) и (1.9) полу­чаем следующие очевидные соотношения.

На основании формулы (1.6)

wx(x, у, г)«вх(х+Дх, У, z)=wy(x, у, z)wy(x, у—Ау, z)= =wz(x, у, z)wz(x, у, z-j-Az) = Rt(r). (1.10) Рис. 1Л1. Составляющие ветра по осям декартовой системы координат в четырех точках поля скоростей ветра

При этом под г понимается та координата, по которой рассмат­ривается корреляционная связь.

На основании формулы (1.7)

wy(x, у, z)wy(x + Ах, у, z)=w.(x, у, г)да2(-* + д*> у, z) =

=wx(*, у, z) wx(х, у 4-by, z)*= wz(л:, у, z) w,(x, у + Ay, z)= =™x(x, У, z)wx(x, y, z-у, z)wy(x, і/, г + Дг) =

= #ЛП (Ml)

На основании формул (1.9) остальные восемнадцать корреляци­онных функций вида wxwy, wyw, и w. wx тождественно равны нулю.

Поскольку в каждой из приведенных в (1.10) и (1.11) корре­ляционных функций изменяется только один аргумент, вычисле-

_ * Чтобы не затемнять чертежи, на рис. 1.11 надписи у проекций вектора w в точках 2 и 3 не сделаны.

ние любой из этих функций производится на основании общей формулы *

X

/?(х)=Нш -±- f{x)f(x+%)dx.

Х-н» М і)

—X

Характер корреляционных функций Rt(r) и Rn(r) был уста­новлен при помощи экспериментов в аэродинамических трубах, в которых создавалась практически однородная и изотропная турбулентность. В результате обработки указанных эксперимен­тов для продольной и поперечной корреляционных функций были получены аппроксимирующие аналитические выражения следующего вида [12]:

Я,(г)=<&е“|г|/ (1.12)

Rn{r)=ol{-rl2L)e-‘r’IL,

где 0%, = W2t = W[5] —среднее

значение квадрата (дисперсия) любой компоненты скорости тур­булентного движения воздуха;

L — так называемый масштаб турбулентности. Непосредственной подстанов­кой можно убедиться, что аппро­ксимирующие формулы (1.12) и

(1.13) удовлетворяют соотноше­нию (1.8).

Графики функций Rt(r) и Rn(r) в нормированной форме

корреляционных функций продоль — приведены на рис. i. iz. jth гра ной и поперечной составляющей фики показывают, что’ масштаб скорости ветра турбулентности L является удоб­

ной характеристикой линейных размеров области, в которой соответствующие составляющие скорости коррелированы заметным образом. Необходимо заме­тить, что масштаб турбулентности L в формулах (1.12) и (1.13) принят одинаковым чисто формально. Из графиков на рис. 1.12. видно, что функция Rn(r) резче спадает к оси абсцисс, чем функ­ция Rt(r). Если определить масштаб турбулентности как инте­грал от нормированной корреляционной функции, то получим следующие значения масштабов для продольной и поперечной корреляционных функций:

ОО во

Lt=-L-^Rt(r)dr=^e-^Ldr=L, (1.14)

Формулы (1.14) и (1.15) показывают, что продольный мас­штаб в два раза больше поперечного. Это обстоятельство всегда нужно иметь в виду при использовании формул (1.12) и (1.13), где оно не отражено в явной форме вследствие применения в обеих формулах одного и того же параметра L.

Поскольку ниже для анализа динамики самолета будут ши­роко использоваться частотные методы, возникает необходимость перейти от корреляционных функций к спектральным плотностям. Спектральная плотность случайного стационарного процесса связана с его корреляционной функцией выражением [6]

5(2)=-l^/?(r)cos2rrfr,

О

где Q — пространственная угловая частота, если г — простран­ственная координата;

Й=2я А. (1.17)

В формуле (1.17) Я есть длила волны спектральных состав­ляющих скорости турбулентного движения воздуха.

Подставляя в (1.16) значения продольной и поперечной кор­реляционных функций из (1.12) и (1.13), получаем выражения для соответствующих спектральных плотностей [7]:

(1.18)

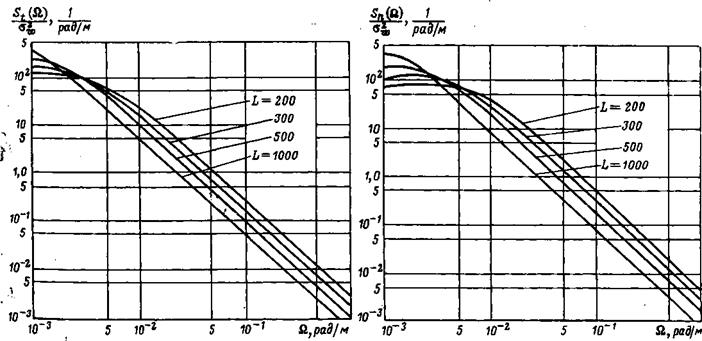
На рис. 1.13 и 1.14 приведены графики нормированных спект­ральных плотностей, построенные по формулам (1.18) и (1.19) для различных масштабов турбулентности L. Сравнение кривых на этих рисунках показывает, что с увеличением масштаба тур­булентности спектральная плотность и, следовательно, мощность и энергия порывов ветра увеличиваются в области низких частот и уменьшаются в области высоких.

Для удобства математических преобразований, ниже будет использоваться так называемая безразмерная частота v, опреде­ляемая формулой

v.-=aL. (1.20)

Рис. 1.13. Графики нормированной спектральной плотности Рис. 1.14. Графики нормированной спектральной плотности продольной составляющей скорости ветра продольной составляющей скорости ветра

Если в выражениях (1.18) и (1.19) для спектральной плотно­сти перейти к безразмерной частоте, то они приобретают вид:

Необходимость изменения постоянного множителя в (1.21) и

(1.22) по сравнению с (1.18) и (1.19) вытекает из тождества

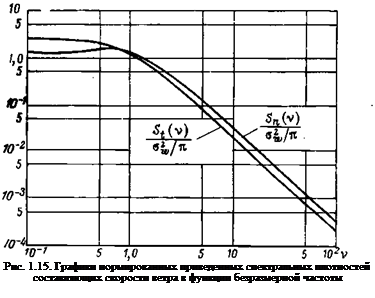al=j S(Q)dQ={S(v)dv, если учесть формулу связи (1.20) между V и Q.

Графики нормированных спектральных плотностей в функции безразмерной частоты, построенные на основании (1.21) и (1.22), даны на рис. 1.15.

Приведенные выше аналитические выражения корреляцион­ных функций и спектральных плотностей для проекции вектора случайного ветра характеризуют лишь пространственное распре­деление поля скоростей ветра. Поэтому эти данные справедливы только для какого-нибудь, пусть произвольного, но одного момен­та времени, для которого поле скоростей является «заморожен­
ным». Между тем, перемещение самолета в пространстве, всегда связано с определенными временными интервалами. Следова­тельно, полученные выше характеристики поля скоростей в тур­булентной атмосфере нельзя безоговорочно использовать для определения возмущений, действующих на самолет. Указанное затруднение можно обойти, используя гипотезу Тейлора [11, 13]. Согласно этой гипотезе поле скоростей турбулентного движения при исследовании динамики самолета может считаться «заморо­женным». В отличие от предыдущего поле считается «заморо­женным» на все время полета, а не для какого-либо одного мо­мента времени. Обоснование гипотезы Тейлора заключается в следующем. Из-за большой скорости полета самолета по сравне­нию со скоростями турбулентного движения воздуха самолет про­летает дистанцию, на протяжении которой корреляционная связь между этими скоростями достаточно сильна, настолько быстро, что за время пролета этой дистанции поле скоростей ветра сколько-нибудь существенно не изменяется. На основании гипо­тезы Тейлора полученные выше аналитические характеристики, справедливые, строго говоря, для одного момента времени, при­меняются для всего времени полета самолета.

Кроме того, если рассматривать самолет как точку [8], движу­щуюся в направлении оси х, то из всех корреляционных функций

(1.10) и (1.11) останутся только три, зависящие от переменной х; остальные переменные (у и г) остаются неизменными и их по этой причине можно опустить. Для продольной составляющей ветра да* на основании (1.10) получаем продольную корреляци­онную функцию

Rtx (*) = да, (*) да, (х+Л*). (1.24)

Для нормальной да„ и поперечной да2 составляющих ветра на основании (1.11) получаем поперечные корреляционные функции:

Rny (•*)=Wy(x)Wy(x + bx), (1.25)

Rm (*) = да2 (х) wz (л: + Дх). (1.26)

Наконец, учтем, что для «замороженного» на все время поле­та самолета поля скоростей ветра существует однозначная связь между пройденным самолетом расстоянием х и временем t:

x=r= Vt. (1.27)

Соотношение (1.27) дает возможность перейти в общих выра­жениях (1.24) — (1.26) для корреляционных функций составляю­щих ветра от пространственной координаты х к временной t. Сле­довательно, такой переход можно сделать и в конкретных ана­
литических выражениях (1.12), (1.13) для этих функций. В ре­зультате замены | г | на V (т) получаем выражения:

Rt(r)=ole~’z’VIL, (1.28)

tfn(*)=4(l-M^/2Z)e-|t, w. (1-29)

Очевидно, что выражение (1.28) относится к составляющей wx, а выражение (1.29) —к составляющим wy и wz.

Пространственные спектральные характеристики поля скорос­тей являются функциями пространственной угловой частоты Q. Временные спектральные характеристики, отражающие процесс взаимодействия этого поля с самолетом, должны, естественно, быть функциями временной угловой частоты to. Эти частоты свя­заны очевидным соотношением

£2х=о)£. (1.30)

Подставляя в (1.30) значение х из (1.27), получаем

Q=<d/V. (1.31)

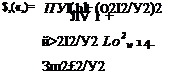Применяя к (1.28) и (1.29) преобразование Фурье, получаем выражения для спектральных плотностей как функции <о:

Формула (1.32) относится к составляющей до*, а формула (1.33) — к составляющим да„ и wz.

Сравнивая (1.32) и (1.33) и с (1.18) и (1.19), а также с (1.21) и (1.22), устанавливаем, что между спектральными плотностями, записанными в различной форме, существует следующая связь:

S(*)=S(Q)IV=S(v)LIV. (1.34)

Рассмотрим, в какой степени приведенные выше аналитиче­ские выражения для корреляционных функций и спектральных плотностей поля скоростей атмосферной турбулентности согла­суются с введенными в § 1.3 понятиями трех интервалов турбу­лентного движения атмосферы. Наиболее удобно для этого вос­пользоваться графиком спектральной плотности, представленной как функция пространственной частоты Q. В качестве примера на рис. 1.16 приведен график продольной спектральной плотности, построенный на основании (1.18), при аю2= 1 м2-сек~2 и L=300.m. На этом графике нанесены границы трех интервалов турбулент­ного движения воздуха. Ясно видно, что в крупномасштабном интервале, занимающем сравнительно узкую часть спектра (если
отложить частоты не в логарифмическом, а в обычном масшта­бе), спектральная плотность почти не зависит от частоты Q или от длины волны A.=2n/Q. Следует заметить, что эта часть спект­ра, полученная из аналитического выражения для изотропной турбулентности, вряд ли может достаточно хорошо отражать процессы в реальной атмосфере, так как известно, что движение воздуха в этом интервале анизотропно. Кроме того, длины волн, большие горизонтальной протяженности турбулентной зоны (см.

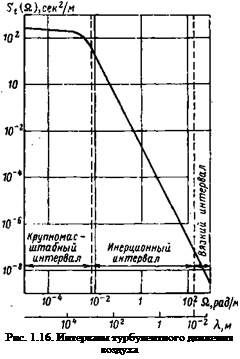рис. 1.7), в реальной ат­мосфере не имеют физиче­ского смысла. Несмотря на указанные недостатки аналитической формулы, применение ее для иссле­дования динамики самоле­та не вызывает существен­ных неточностей, так как влияние длинноволновых ветровых возмущений на самолет очень невелико. Как правило, измерение результатов этого влия­ния лежит за пределами возможностей самолет­ной измерительной аппа­ратуры.

Инерционный диапа­зон в логарифмических координатах характеризу­ется линейной зависимо­стью спектральной плот­ности от пространствен­ной частоты, что соответ­ствует степенной функции (см. рис. 1.16).

В введенных в этом параграфе аналитических выражениях

(1.18) и (1.19) спектральная плотность в инерционном диапазоне практически пропорциональна Q-2.

На рис. 1.16 наклон кривых спектральной плотности на участ­ке вязкого интервала такой же, как и на участке инерционного интервала. Это противоречит теоретическим оценкам спектра в вязком интервале, согласно которым наклон кривых должен быть значительно большим, чем в инерционном интервале. Отмеченный недостаток используемых здесь аналитических формул для атмос­ферной турбулентности связан с желанием получить как можно более простые и поэтому удобные для расчетов выражения.

Стремление к упрощению привело также к тому, что выраже­ния (1.12) и (1.13) для корреляционных функций не дают нуле­
вого значения для производной при г=0. При переходе через значение г—0 производная от корреляционной функции изменяет­ся скачком. Например, в (1.12) при подходе справа к нулю

tdRi <сМ _———— Е— а при подходе слева (- -(г) ) =

dr }г=0- L dr )г~

4 О

_ ”w Указанное обстоятельство поясняется рис. 1.17.

L

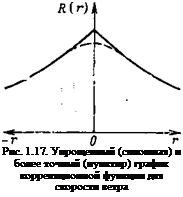Корреляционная функция для производной от случайной функции определяется как вторая производная от корреляцион­ной функции для самой случайной функции. Поэтому вторая про­изводная от корреляционной функции для скорости соответ­ствует корреляционной функ­ции для ускорения частиц воз­духа при турбулентном движе­нии.

Так как упрощенное описа­ние корреляционной функции для скорости турбулентного движения воздуха приводит к появлению скачка в значении для первой производной от этой функции при г=0, то, очевидно, что вторая производная от нее, т. е. корреляционная функция для ускорения частиц воздуха будет содержать импульсивную функцию (6-функцию) при г=0. Как указано в «Приложении D», в этом случае дисперсия случайного процесса будет равна беско­нечности, что не. может иметь место для реальных процессов. По­лучение бесконечного значения дисперсии для ускорения частиц воздуха турбулентного движения является следствием отмеченно­го выше упрощения при аналитическом описании корреляционной функции для скорости турбулентного движения.

При более резком спаде спектра в вязком интервале указан­ное .противоречие устраняется, и график корреляционной функ­ции для скорости ветра вблизи значения г=0 получает вид, по-

казанный на рис. 1.17 пунктиром. В этом случае

Приближенное аналитическое выражение для участка корреля­ционной функции R(r) вблизи г=0, связывающее характер корреляционной функции на этом участке с масштабом турбу­лентных движений воздуха в вязком интервале, можно найти в работе [7].

Приведенные выше аналитические выражения для корреля­ционных функций и спектральных плотностей продольной и попе­
речной составляющих вектора случайной составляющей скорости ветра, как указывалось, найдены в результате обработки экспери­ментальных данных, полученных при исследовании турбулент­ности в аэродинамических трубах. Теоретическая оценка спек­тральной плотности в инерционном диапазоне, выполненная впервые А. Н. Колмогоровым [14], дает результаты, несколько отличные от приведенных выше. В соответствии с этой оценкой спектральная плотность в инерционном диапазоне должна быть пропорциональна Q-5/3.

На основании этого Карман [50] предложил следующие фор­мулы для продольной и поперечной корреляционных функций и спектральных плотностей поля скоростей турбулентного движе­ния воздуха.

Корреляционные функции:

*"<‘>=’•=7^у(тягГ [К»- Стшг)-

2~( і, з.т )к,/,( 1,3391 )]’ О-36)

где L — масштаб турбулентности;

Кч, (г), АТ«/, (г) — модифицированные функции Бесселя дроб­

ного порядка;

Г (л:) — гамма-функция.

Коэффициент 23/я/Г(!/з) равен 0,59253. Для сравнения на рис. 1.18 приведены графики поперечных корреляционных функ­ций, построенные на основании выражения (1.13) (пунктир) и выражения (1.36) (сплошная). Сравнение графиков показывает, что эти корреляционные функции незначительно отличаются друг от друга.

Спектральные плотности, соответствующие (1.35) и (1.36), имеют вид:

St (2)=Ода=— Л л I	2	(1.37)
[1+(1,33912)2]5/6 8 1 + — (1,339LQ)2
5Л(2)_^ —	3 [1 + (l,339iQ)2]U/6	(1.38)

Для инерционного диапазона масштабов турбулентного дви­жения, т. е. при значениях 1,339 LQ>1, формулы (1.37) и (1.38)
уменьшение опектральной плотности с увеличением час­тоты в вязком диапазоне;

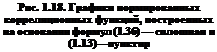2) скачкообразное измене­ние производной от корре­ляционной функции при пере­ходе через значение г=0.

В работе [48] указывается, что при очень тщательной об­работке экспериментальных данных по атмосферной турбу­лентности, корреляционные функции и спектральные плот­ности для поперечной состав­ляющей скорости случайного ветра несколько лучше аппрок­симируются выражениями (1.35)—(1.38), чем выражениями

(1.12) — (1.15). Однако следует отметить, что в зависимости от ме­теорологических условий экспериментально получаемые спект­ры атмосферной турбулентности имеют довольно большой раз­брос значений показателя степени у Q на инерционном интервале, вследствие чего незначительное различие между аппроксимация­ми (1.12)—(1.15) и (1.35) — (1.38) не имеет для большинства за­дач динамики полета существенного значения. Кроме того, вы­ражения (1.12) — (1.15) выгодно отличаются от выражений (1.35) — (1.38) своей простотой. Это обстоятельство существенно облегчает аналитические исследования движения самолета в тур­булентной атмосфере при использовании формул (1.12) —(1.15), а также моделирование этого движения на аналоговых машинах. По указанным причинам в данной книге будут использоваться формулы (1.12) — (1.15).

Если анализ динамики полета в турбулентной атмосфере ве­дется на цифровых вычислительных машинах, то использование формул (1.35) — (1.36) не вызывает никаких затруднений.

В заключение этого параграфа укажем, что мгновенные зна­чения компонент вектора скорости ветра в атмосфере считаются распределенными по нормальному закону. Для любой из компо-

нент скорости ветра (например, для а*х) плотность вероятности имеет вид *

<У-У0х)’

/(«»,)=——— Х~7=~е ’ 0-39)

<ywV 2я

где W0x — постоянная составляющая скорости ветра в направ­лении оси х.

Ниже будут приведены экспериментальные результаты, под­тверждающие справедливость нормального закона распределения для мгновенных компонент скорости ветра.